Power Tower -- from Wolfram MathWorld
5 (568) · € 45.99 · En stock
The power tower of order k is defined as a^^k=a^(a^(·^(·^(·^a))))_()_(k), (1) where ^ is Knuth up-arrow notation (Knuth 1976), which in turn is defined by a^^nk=a^^(n-1)[a^^n(k-1)] (2) together with a^k = a^k (3) a^^n1 = a. (4) Rucker (1995, p. 74) uses the notation ^ka=a^(a^(·^(·^(·^a))))_()_(k), (5) and refers to this operation as "tetration." A power tower can be implemented in the Wolfram Language as PowerTower[a_, k_Integer] :=

Power Tower -- from Wolfram MathWorld

Power Tower -- from Wolfram MathWorld

Power Tower -- from Wolfram MathWorld

Power Tower -- from Wolfram MathWorld

Power Tower -- from Wolfram MathWorld
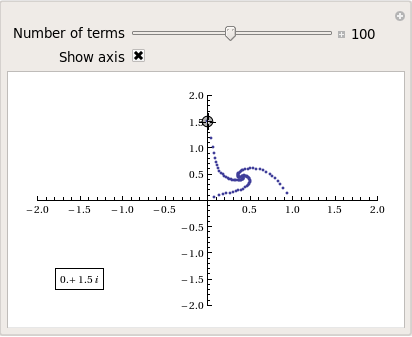
Complex Power Towers (Or 'mucking around with Mathematica')
Integral involving up-arrow notation
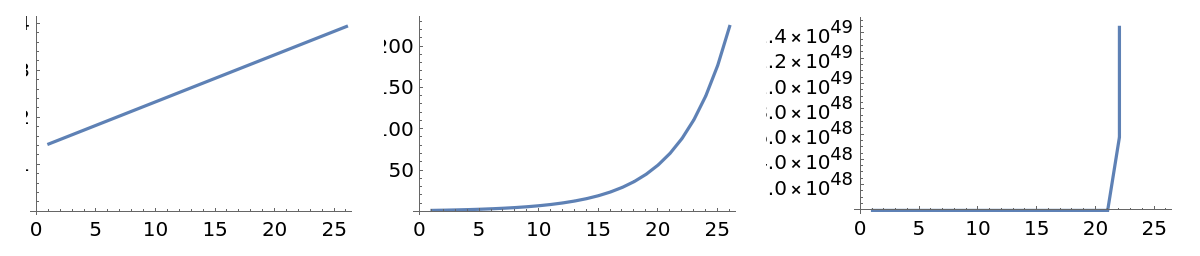
Tetration Wolfram Function Repository

Power Tower -- from Wolfram MathWorld

Power Tower -- from Wolfram MathWorld
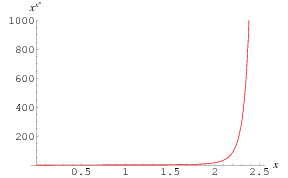
Power Tower

1908.05559] The strange properties of the infinite power tower An “investigative math” approach for young students












